計算量理論入門

前回の講義では、「多項式時間/空間」という測量を導入し、時間 (= '手数') と空間 (= 'working storage') という制限が、問題の難しさを量るのに本質的であることを確認し、様々な問題の難しさを新しく見直しました。

復習すると、ある問題が容易に解ける (= 多項式時間認識可能である) というのは、'1つでも' 多項式時間で解ける方法 (= 機械) があればよかったわけです。
一方で、そのような機会が存在しないことを示すためには、'どんな方法でも' 解けないということをいわなければならないわけなので、そういった部分に数学的な証明の難しさがあります。

単独での証明はむずかしい -- そこで考えるのが最終日のテーマ「帰着」です。

Definition. (Polynomial-time reduction)
言語 $A$ が言語 $B$ に 多項式時間帰着する とは、多項式時間機械 $T$ が存在して、任意の入力 $x$ に対する $T$ の出力 $T(x)$ が $x \in A \Longleftrightarrow T(x) \in B$ を満たすことをいう。 $~~~~~ \bigcirc$

$A$ が $B$ に多項式時間で帰着することを

$A \leq^\mathrm{P} B$

と書きます。このようにして「問題の難しさを相対的にとらえる」ことが大事です。

また、この不等号 $\leq^\mathrm{P}$ は '多項式時間 (Polynomial time)で $A$ の難しさは $B$ 以下' であることを示しているのでこのような順番になっています。(ところで、僕が[歴史]言語学の記法で一番気に食わないのは

$\mathrm{rational} < \mathrm{rationem} < \mathrm{ratio}$

-- のように*1、"右辺は左辺を導く" ということを示す '<' の使い方です。数学にふけっていたころ言語学が好きではないとか言っていたのにはこういう文化的な違いへの戸惑いがあったのです。)

Frobenius 写像の周辺

昨日までは有限体 $\mathbb{F}_p$ という領域で様々な現象を観察してきました。最終日は講義の '周辺' の部分をみていきます。具体的には次の2つ:

Frobenius 持ち上げ: -- Frobenius 写像の、標数が $p$ でない場合の類似物
δ 環: -- 「あまりの構造」(= たし算とかけ算の振る舞い) を用いた ``環構造の復元"

まず、Frobenius 写像を考えることのうれしさというのは、たし算とかけ算について特別な性質を持っていた (= '環準同型' であった) ためだったことを思い出し、したがって Frob. 持ち上げ $\phi$ にも同じ条件をまず課します。

また、この持ち上げという操作に Frobenius-like な性質を与えるため、 $\mathrm{mod} ~ p$ で考えたときのあまりを考察します。ここで、

$\phi (a) ~~~ = ~~~ a^p + (p$ の倍数 $)$

とすると、 $\delta$ 構造というのはこの「 $\mathrm{mod} ~ p$ でのあまり」について満たすべき性質を公理化したもの、とおくことができます。

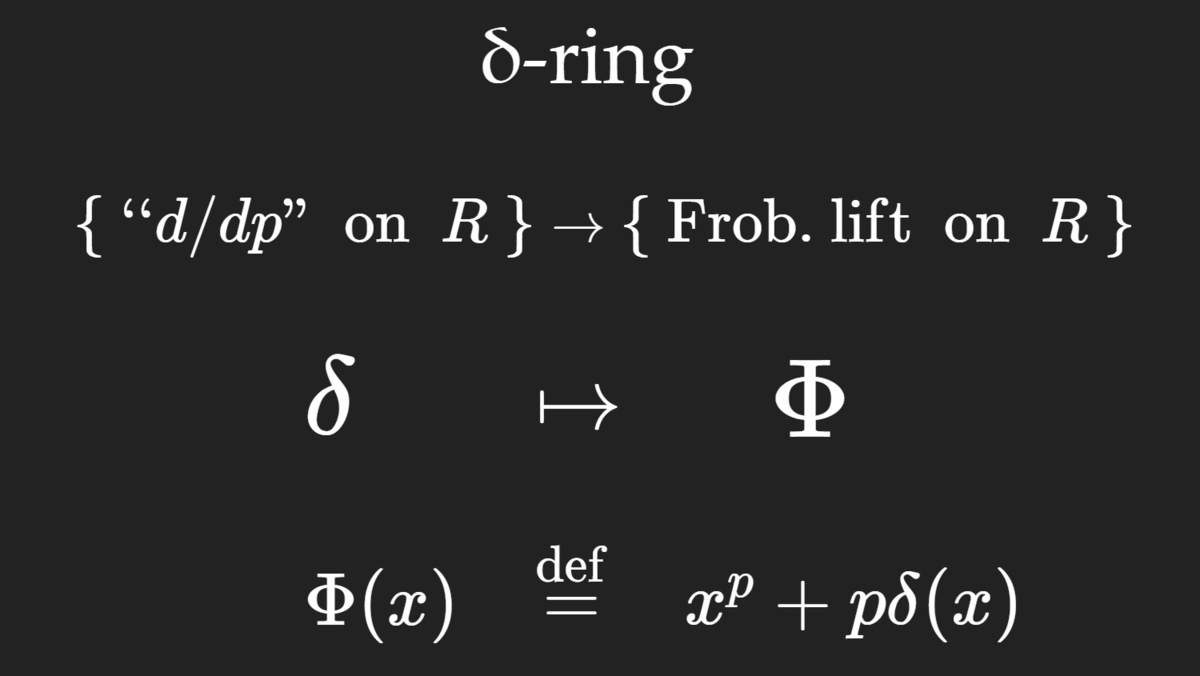
f:id:zeta_aniki:20210806013252p:plain — *δ-ring*

これは、1985年に André Joyal という数学者が厳密な定義を与えたもので、近年では

$q$ -de Rham cohomology
prismatic cohomology

という対象を研究する上で盛んに取り扱われているそうです。とくに prismatic cohomology というのは Peter Scholze & Bhargav Bhatt によって定義され、2016年あたりから数論幾何の分野でたくさん注目を集めているということで、まさに最先端の (!) 研究対象だといえそうです。

ここで、 $\delta$ 環の周辺について読むことのできる文献をまとめておきます。

まず、A. Joyal による原論文 (1985年):

https://maths-people.anu.edu.au/~borger/classes/copenhagen-2016/references/joyal1.pdf

James Borger の Course on Witt vectors, lambda-rings, and arithmetic jet spaces:

https://maths-people.anu.edu.au/~borger/classes/copenhagen-2016/index.html

講義の初日の映像 (特に ~10分前後):

www.youtube.com